Last Updated on January 17, 2025
FREE MCAT Practice Test 2025 Official AAMC Study Guide [PDF]. Get our free Medical College Admission Test (MCAT) practice questions and answers in a printable PDF. This comprehensive resource is designed to help you prepare for the MCAT, administered by the Association of American Medical Colleges (AAMC).
GoTestPrep provides extensive MCAT test prep and review questions featuring key subject-specific strategies. Additionally, we offer two full-length practice tests followed by thorough explanations to enhance your understanding and improve your performance.
The Medical College Admission Test (MCAT) is a standardized exam used to assess medical school applicants. The Association of American Medical Colleges (AAMC) sponsored the test in cooperation with its member schools.
Most U.S. medical schools require it as part of the admissions process. Prometric, a private firm that provides technology-based testing and assessment services, administers the test.
Gaining admission to a U.S. medical school can be incredibly challenging if you are not a U. S. citizen. In recent years, fewer than one percent of first-year med students were non-U.S. citizens. Most of these students attended college in the United States before applying to medical school.
The Medical College Admission Test (MCAT) is a computer-based standardized examination for prospective medical students in the United States, Australia, Canada, and the Caribbean Islands.
MCAT Practice Test 2025
Medical schools use MCAT scores to assess whether you possess the foundation to build a successful medical career. Though you certainly need to know the content to do well, the stress is on the thought process because the MCAT is, above all else, a thinking test. It emphasizes reasoning, critical and analytical thinking, reading comprehension, data analysis, writing, and problem-solving skills.
AAMC MCAT Questions Answers
(59 MCQs Biological and Biochemical Foundations of Living Systems)
(59 MCQs Psychological, Social, and Biological Foundations of Behavior)
(59 MCQs Chemical and Physical Foundations of Biological Systems)
(53 MCQs Critical Analysis and Reasoning Skills)
AAMC MCAT Exam Format 2025
The MCAT questions are designed to measure your problem-solving and critical-thinking skills. Two test sections assess your mastery of fundamental biology, biochemistry, general chemistry, organic chemistry, and physics concepts. A third section tests your understanding of psychology, sociology, and biology concepts that are important to understanding how behavioral and sociocultural factors affect health outcomes and healthcare provision.
For most questions in these sections, choosing the correct answer requires more than just a rote response; you must calculate a solution, interpret and evaluate given data, or apply a particular scientific principle to a given situation.
You must demonstrate that you can reason scientifically and employ the principles of research methodology and statistics. A fourth section tests your ability to analyze, evaluate, and apply information from reading passages on topics in ethics, philosophy, cross-cultural studies, and population health.
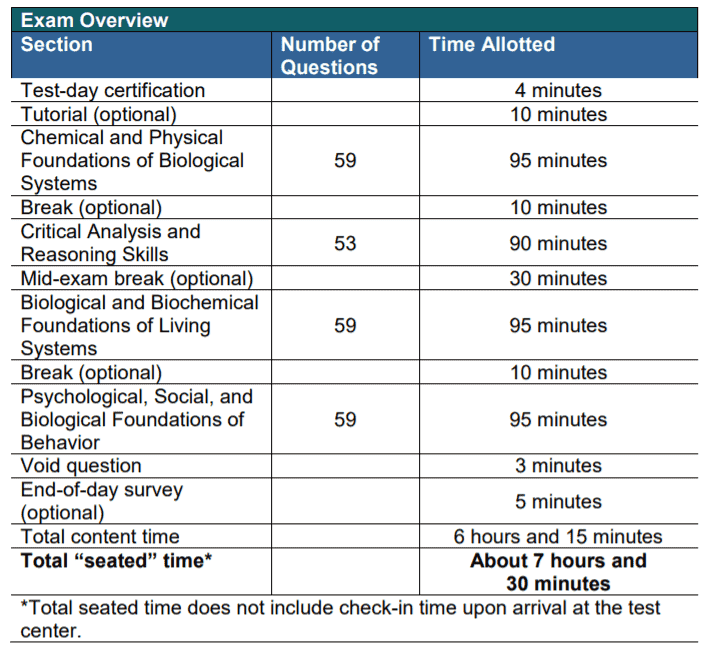
The current MCAT consists of four distinct sections that are individually scored. Each section is allotted 90 or 95 minutes and tests between 50 and 60 questions. Including breaks, the full examination lasts approximately 7.5 hours.
| Section | Questions | Minutes |
|---|---|---|
| Chemical and Physical Foundations of Biological Systems | 59 | 95 |
| Critical Analysis and Reasoning Skills | 53 | 90 |
| Biological and Biochemical Foundations of Living Systems | 59 | 95 |
| Psychological, Social, and Biological Foundations of Behavior | 59 | 95 |
1. Chemical and Physical Foundations of Biological Systems Question Format
The Chemical and Physical Foundations of Biological Systems section includes:
59 questions consisting of:
- 10 passage-based sets of questions
- 4-6 questions per set
- 15 independent questions
2. Critical Analysis and Reasoning Question Format
The Critical Analysis and Reasoning Skills section includes:
53 questions consisting of:
- 9 passages
- 5-7 questions per passage
3. Biological and Biochemical Foundations of Living Systems Question Format
59 questions consisting of:
- 10 passage-based sets of questions
4-6 questions per set
15 independent questions
4. Psychological, Social, and Biological Foundations of Behavior Question Format
The Psychological, Social, and Biological Foundations of Behavior section includes:
59 questions consisting of:
- 10 passage-based sets of questions
4-6 questions per set - 15 independent questions
MCAT Score
The test consists of four sections, each scored from 118 to 132 with a median score of 125. The total MCAT score is a sum of the scores from each of the four sections, ranging from 472 to 528, with a median score of 500. Scores are released on a pre-determined date between 30–35 days after the exam.
You will receive a separate score and a total score for each of the four sections of the MCAT exam.
- Your raw score on the four multiple-choice sections is based on the number of questions you answer correctly in each section. There is no penalty for guessing.
- The raw score for each section is then converted to a scaled score ranging from 118 (lowest) to 132 (highest).
- Your total scaled score is the sum of the four individual section scores and will range from 472 to 528
Please visit our MCAT scores webpage for additional information on exam scoring, including a short video and an example of a score report.
Official MCAT Study Guide 2025
There’s no such thing as a cut-and-dry “good score.” Much depends on the strength of the rest of your application (if your transcript is first-rate, the pressure to strut your stuff on the MCAT isn’t as intense) and where you want to go to school (different schools have different score expectations). Here are a few interesting statistics:
It’s important to maximize your performance on every question. Just a few questions, one way or the other, can make a big difference in your scaled score. Here’s a look at recent score profiles to get an idea of the shape of the typical score distribution.
The average student spent 12 weeks preparing for the MCAT exam, spending about 23 hours per week, excluding time taking regular courses. Some students, however, choose to take more time.
Another popular student study option is using a commercial company’s MCAT preparatory materials. Many companies provide preparatory classes in person and online and sets of preparatory books, full-length practice exams, flashcards, and more. 77% of students used commercial preparation books, and 67% used practice exams published by a commercial company. 85% of test-takers found MCAT prep books helpful.
Official MCAT Prep Link: aamc.org/prepare-mcat-exam
Download The MCAT® Essentials for Testing Year 2025 [PDF Link] (The MCAT® Essentials Addendum for the January and March 2021 Exams)
AAMC customer service
MCAT Program
AAMC
655 K St. NW, Suite 100
Washington, DC 20001-2399
Telephone: 202-828-0600
Contact Form: aamc.org/contactmcat
Hours:
Monday-Friday, 9 a.m.-7 p.m. ET
Closed Wednesday, 3-5 p.m. ET