Last Updated on November 28, 2024
PSAT 8/9 Math Practice Test 2024 (38 Questions and Answers): Try our free Preliminary SAT/National Merit Scholarship Qualifying Test review mathematics questions and answers. There are a total of 38 multiple-choice questions with answer keys and explanations. You can also download it as a printable PDF for a worksheet.
PSAT 8/9 Math Practice Test 2024
| Test Name | PSAT 8/9 Practice Test 2025 |
| Sections | Mathematics |
| Total Items | 38 MCQs |
| Test Type | Sample Online Test |
| Time Limit | NO |
| Answer Keys/ Explanation | Available |
Q1. If y + 3 = 7, what is the value of 2y + 3 ?
- (A) –5
- (B) 8
- (C) 11
- (D) 14
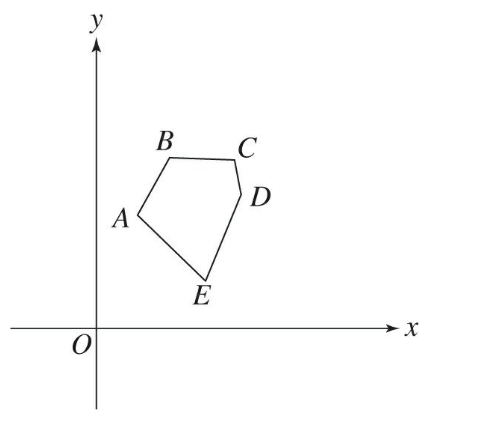
Q2. In the figure above, which side of 5-sided polygon ABCDE has the greatest negative slope?
- (A) EA
- (B) AB
- (C) BC
- (D) CD
Q3. Rhys has a bucket of candy containing 15 lollipops, 25 gumballs, 35 licorice sticks, and no other types of candy. If Rhys selects one type of candy at random, what is the probability that the chosen candy will be a licorice stick?
- (A) \frac{1}{5}
- (B) \frac{1}{3}
- (C) \frac{3}{10}
- (D) \frac{7}{15}
Q4. If (b + 2)(3b – 6) = z, then (b + 2)(b – 2) = ?
- (A) \frac{1}{6}z
- (B) 3x
- (C) \frac{1}{3}z
- (D) \frac{1}{2}z
Q5. If three lines intersect to form six equal angles, what is the measure of one of these angles?
- (A) 15°
- (B) 30°
- (C) 45°
- (D) 60°
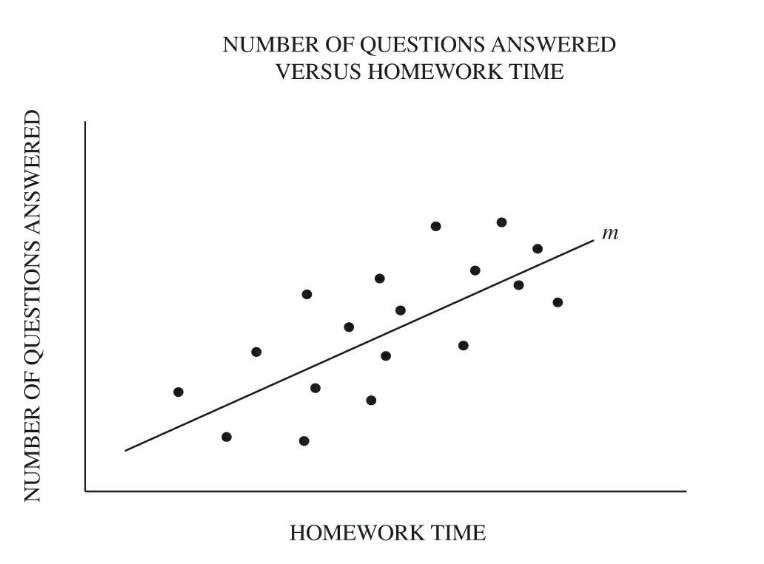
Q6. Brian surveyed the 18 students in his algebra class to determine the amount of time they spent doing homework and the number of questions answered on the last test. The scatterplot above shows the homework time and the number of test questions answered for each of the 18 students. Line m is the best fit line. For how many students was the number of test questions answered fewer than what the best fit line predicted for the corresponding homework time?
- (A) 8
- (B) 9
- (C) 10
- (D) 11
Q7. The expression 3p + 6 could be represented by which of the following operations?
- (A) 3 times 6 more than a number p
- (B) 3 times 6 less than a number p
- (C) 3 more than 6 times a number p
- (D) 6 more than 3 times a number p
Q8. If the quantity (2t – 5) is divisible by t, which of the following could be the value of t ?
- (A) 4
- (B) 5
- (C) 6
- (D) 7
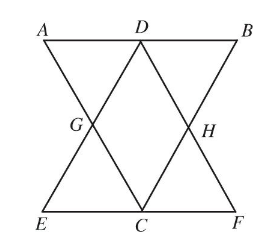
Q9. In the figure above, AD = DB = EC = CF. If ΔABC and ΔDEF are equilateral, and AB = 10, what is the perimeter of quadrilateral CGDH?
- (A) 10
- (B) 15
- (C) 20
- (D) 25
- (E) 35
Q10. Helene lists her zip code on an application form. She notices that the first and last digits are both prime, the middle digit is a divisor of 45, and the least common multiple of the remaining two digits is 6. Which of the following numbers could be her zip code?
- (A) 22935
- (B) 23924
- (C) 32437
- (D) 35563
Q11. What number is 4 less than \frac{1}{2} of itself?
- (A) –11
- (B) –10
- (C) –9
- (D) –8
Q12. Ringo is a dog that is not brown. From which of the following statements can it be determined whether or not Ringo is a Labrador?
- (A) Any dog that is not brown is not a Labrador.
- (B) Some dogs that are brown are not Labradors.
- (C) All dogs that are brown are Labradors.
- (D) No dogs are both brown and Labradors.
Q13. The side of square S is twice the diameter of circle C. What is the greatest possible number of points of intersection of the perimeter of square S and the circumference of circle C ?
- (A) Two
- (B) Three
- (C) Four
- (D) Six
Q14. If the ordered pair (t, 2), where x = t and y = 2, is the intersection of the two lines above, then what is the value of n ?
y = –x
y = x + n
- (A) –2
- (B) 0
- (C) 2
- (D) 4
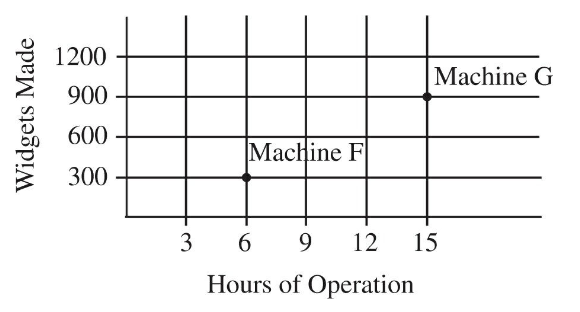
Q15. The graph above shows the number of widgets made by two machines, F and G, plotted against the number of hours in operation. On average, for each hour of operation, how many more widgets did machine G make than machine F?
- (A) 9
- (B) 10
- (C) 22
- (D) 50
Q16. If w is an integer and 8 is a factor of 2w, which of the following must be true?
I. w is an even integer
II. w is divisible by 4
III. w is divisible by 8
- (A) I only
- (B) II only
- (C) I and II only
- (D) II and III only
- (E) I, II, and III
Q17. If q and s are greater than 0 and \frac{q¹²}{q²} = s5, then = \frac{s¹²}{s²}
- (A) q5
- (B) q6
- (C) q10
- (D) q20
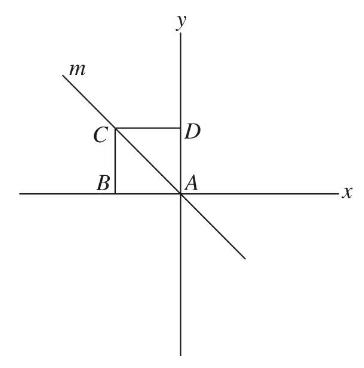
Q18. Line l, defined by the equation x + 2y = 4, is graphed in the xy-plane. Line m is the reflection of line l across the x-axis. Which is the following is an equation of line m ?
- (A) x – 2y = –4
- (B) x + 2y = –4
- (C) x – 2y = 4
- (D) x + 2y = 4
Q19. A lock requires a 3-digit code such that each digit is a positive even number less than 9. How many such codes are possible?
- (A) 4
- (B) 8
- (C) 16
- (D) 64
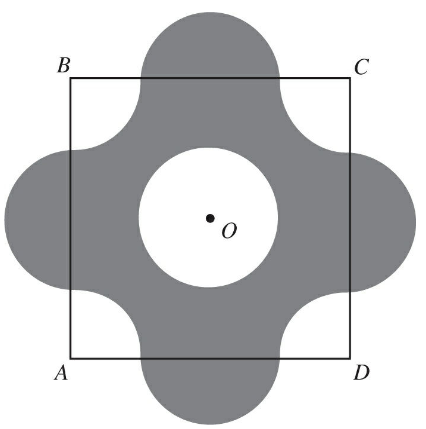
Q20. The figure above shows a square with side of length 4. The center of the square, point O, is also the center of circle O, with radius 1. Four semicircles with radius 1 are centered on each side of the square. If the arcs shown have centers at A, B, C, and D, what is the area of the shaded region?
- (A) 4π
- (B) 16
- (C) 8π – 8
- (D) 8 + 4π
Q21. If r is an integer and 7.3 × 10r is a number between 8,000 and 80,000, what is the value of r ?
- (A) 1
- (B) 2
- (C) 3
- (D) 4
Q22. In the xy-plane above, ABCD is a square with a side length of 8. If line m passes through points A and C, which of the following points lies on line m ?
- (A) (–5, 0)
- (B) (0, –5)
- (C) (–5, 5)
- (D) (0, 5)
Q23. A total of 30,000 students attend College Q. How many of the students have a GPA that is less than 4.0 ?
- (A) 3,000
- (B) 6,000
- (C) 12,000
- (D) 24,000
3, 15, 35, 63, …
Q24. The sequence above is formed by multiplying each odd integer by the next odd integer, starting with 1. What is the difference between the 7th and 8th term of the sequence?
- (A) 1
- (B) 28
- (C) 60
- (D) 128
Q25. When Gilbert rents a car from the Cars4U dealership, he is charged a constant rate per mile the car is driven plus a fixed cost for a carwash. On Monday he was charged a total of $13 after driving the rental car for 20 miles. On Friday he was charged $11.50 for driving the rental car 14 miles. Which of the following equations expresses the total charge T, in dollars, when Gilbert drives the rental car for m miles?
- (A) T = m – 7
- (B) T = 0.25m
- (C) T = 0.25m + 8
- (D) T = 0.5m + 4
Q26. The function g is defined by g(x) = 33 – 4x. If g(b) = 5, what is the value of b ?
- (A) \frac{19}{2}
- (B) -7
- (C) 7
- (D) \frac{19}{2}
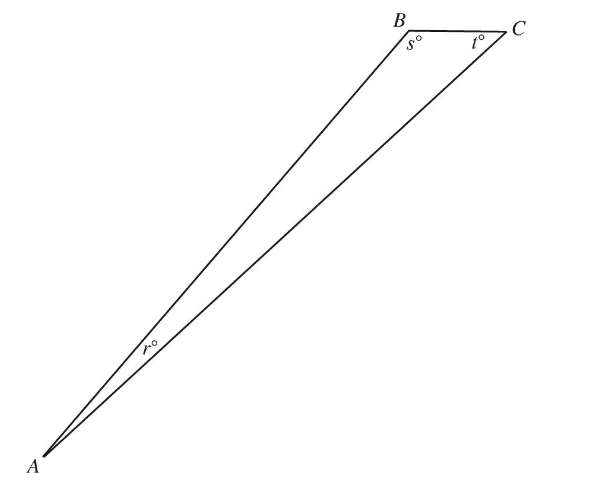
Q27. In the figure above, AB = 200 and BC = 5. Which of the following must be true?
- (A) r is less than s and t
- (B) s is greater than r and t
- (C) t is greater than r and s
- (D) s is equal to t
Q28. At a certain department store, the only sizes of shirts sold are small, medium, and large. At that store, the ratio of small shirts to medium shirts is 5:2, and the ratio of medium shirts to large shirts is 6:5. What is the ratio of small shirts to all other shirts?
- (A) 5:11
- (B) 5:16
- (C) 7:11
- (D) 5:11
Q29. Each of the 8 salesmen at a used car dealership met his sales quota of 5 cars last month. In addition, 3 of the salesmen each sold exactly 3 additional cars, and 2 of the salesmen each sold 1 additional car. What is the total number of cars sold by these 8 salesmen?
- (A) 11
- (B) 21
- (C) 41
- (D) 51
Q30. In 1976 the world record distance for throwing a discus was 230 feet, and by 1983 the record distance had increased to 235 feet and 3 inches. If the record distance continues to increase at the same rate, in what year will the record distance for throwing a discus reach 261 \frac{1}{2} feet?
- (A) 18
- (B) 118
- (C) 1,018
- (D) 2,018
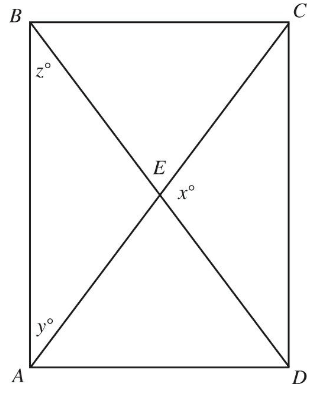
Q31. In the figure above, what is the value of z ?
- (A) 1
- (B) 10
- (C) 11
- (D) 110
Q32. In the figure above, AC and BD are the diagonals of rectangle ABCD. If x = 123, what is the value of z ?
- (A) 28.5
- (B) 25.5
- (C) 38.5
- (D) 48.5
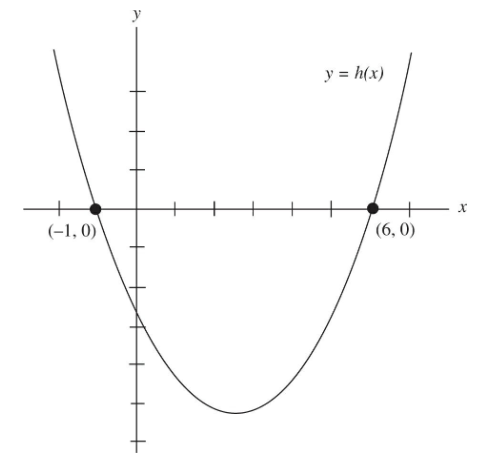
Q33. In the graph above, h(x) is a quadratic function. For what x value does h(x) reach its least value?
- (A) 1.5
- (B) 2.5
- (C) 6.5
- (D) 12.5
Q34. On her first four quizzes, Jan score 12, 8, 1, and 15 points. After Jan took her fifth quiz, she found that the average (arithmetic mean) of the five quiz scores was equal to the median of the five quiz scores. What is one possible value for the number of points Jan scored on her fifth quiz?
- (A) 2, 3, 8
- (B) 1, 9, 14
- (C) 3, 3, 21
- (D) 4, 9, 24
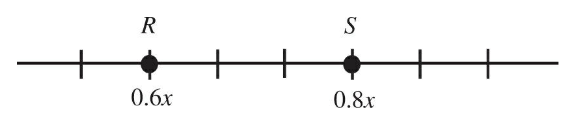
Q35. On the number line above, the distance between point R and point S is 3. What is the value of x?
- (A) 3
- (B) 15
- (C) 25
- (D) 35
Q36. Sara created a list of 500 consecutive multiples of 4. What is the result if Sara subtracts the smallest number in her list from the largest number her the list?
- (A) 1233
- (B) 1195
- (C) 1996
- (D) 3596
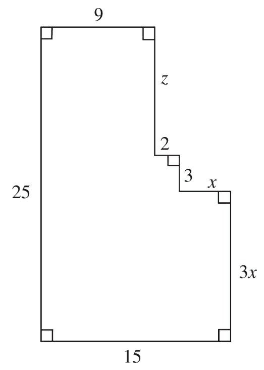
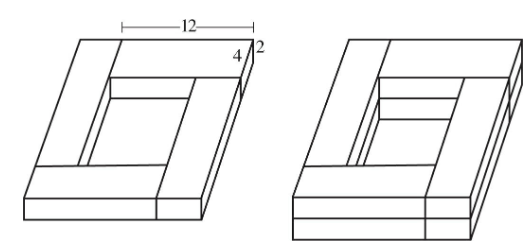
Q37. Four boards each measuring 2 inches by 4 inches by 12 inches are laid on a flat floor to form a square, as shown in the figure on the left. Another four boards of the same dimensions are laid on top of the first four in the same way, as shown in the figure on the right. This process is repeated until the boards are stacked a total of 10 boards high. The box created by these boards is then filled with sand until the sand is perfectly level with the highest point of the box. What is the volume, in cubic inches, of the sand in the box?
- (A) 1,280
- (B) 1,490
- (C) 1,690
- (D) 1,990
Q38. If 5< \frac{80}{x+2} <6 , then what is one possible value of \frac{40}{x+2} ?
- (A) 0.5
- (B) 2.5
- (C) 12
- (D) 15.5